考慮有 \(N\) 個尚未衰變的原子核，在此後一段很短的時間 \(\Delta t\) 內，其數目將改變 \(\Delta N\)。由於數目是在減小，\(\Delta N\) 為負數。根據上一節中，單位時間內發生衰變的原子核數目正比於尚未衰變的原子核數，可以得到以下關係 \[\frac{\Delta N}{\Delta t}=-k\,N\] \(k\) 為衰變常數。運用微積分，我們可以得到 \(N\) 隨時間衰減的形式為指數函數 \[N=N_0\,\textrm{e}^{-k\,t}\] 其中 \(N_0\) 為初始時刻 \(t=0\) 時，未衰變原子核的數目。不難驗證，\(N\) 對時間 \(t\) 的導數 \[N'=-k\cdot N_0\,\textrm{e}^{-k\,t}=-k\,N\] 正比於未衰變的原子核數。

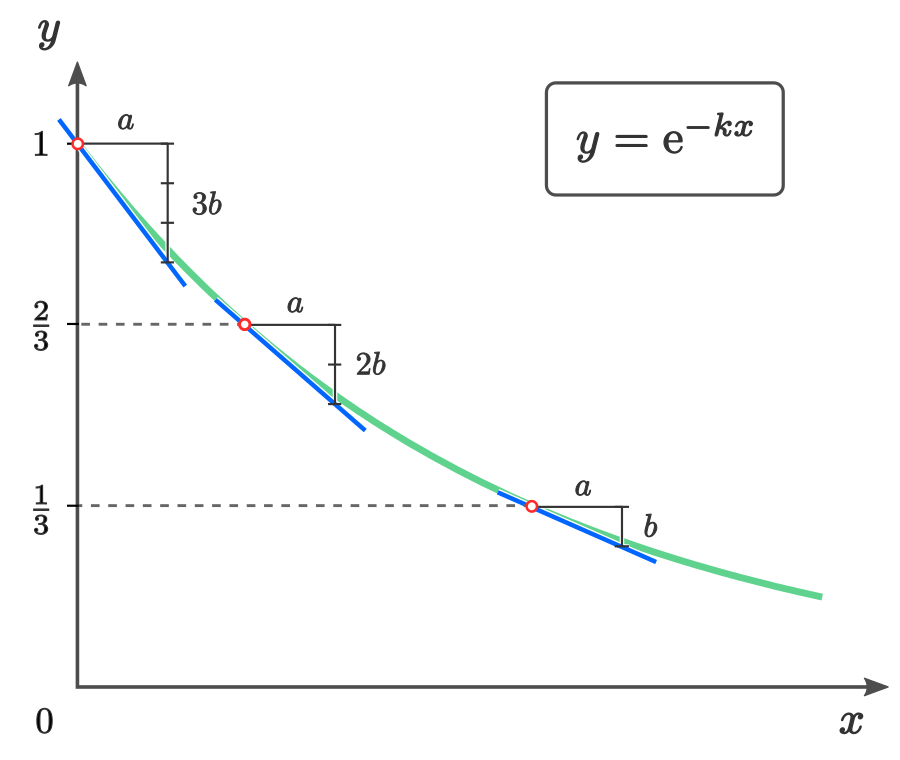
對於指數形式的衰減，有趣的是，每經過一段特定的時間 \(T\)，未衰變的原子核數目都會減少至一個固定的比例，即 \[\frac{N(t+T)}{N(t)}=\frac{N_0\,\mathrm{e}^{-k\,(t+T)}}{N_0\,\mathrm{e}^{-k\,t}}=\mathrm{e}^{-k\,T}\] 我們將未衰變的原子核數目減少為 1/2 所需的時間稱為半衰期，記為 \(T_{1/2}\)。由 \[\mathrm{e}^{-k\,T_{\,1/2}}=\frac{1}{2}\] 不難得出 \[T_{1/2}=\frac{\ln 2}{k}\] 半衰期只與衰變常數 \(k\) 有關。不同種類的放射性核素有不同的半衰期。

放射性核素的放射強度正比於未衰變的原子核數，所以放射強度同樣是以指數形式衰減。每經過一個半衰期，放射強度就會減半（見）。